non-Hermitan Physics and Magnons

Dec 1, 2024

update Dec 2024: We have been awarded a highly competitive Marsden Award to study this topic for another three years (2025-2028)!

Resonances normally exhibit either gain or loss due to their interactions with the environment. This means that the Hamiltonian of the system is no longer Hermitian, a situation that leads to a range of interesting physics. In particular, coupling two non-Hermitian resonances together leads to the emergence of the so-called exceptional point, a topological feature at which both eigenvectors and eigenvalues coalesce.

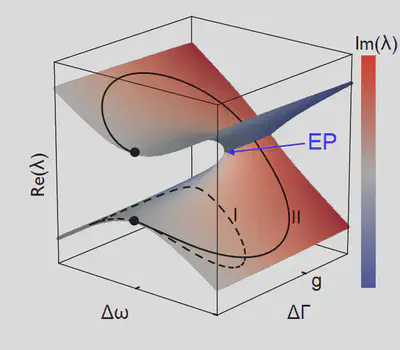
We propose that the non-Hermitian physics of cavity-magnonic systems is a useful approach for coherent control. Cavity-magnonics involves coupling microwave frequency electromagnetic excitations (for example, in 3D cavities) to magnons supported by ferromagnetic or antiferromagnetic systems. This is a versatile platform, as a range of materials and structures can be used to support both of these resonant modes. The microwave modes can also be used as a ‘cavity bus’ allowing spatially separated objects to be coupled.

Two YIG spheres are positioned at the magnetic field antinodes of the second harmonic of a transmission line cavity. Two sources, at $ω\_p$ and $ω\_d$ , are coupled into the cavity. The transmitted amplitude and dispersive phase shift at ωp is measured by homodyne detection. A global field, $H\_0$, is applied to align the magnetization of the spheres in the propagation direction of the cavity, and tune the ferromagnetic resonance to be off-resonance with the cavity modes. The field at each sphere is adjusted by $±δH/2$ using a local coil wrapped around the cavity. (b) Energy level diagram. The lowest two cavity modes are at $ω\_1$ and $ω\_2$. The spatially separated magnets have magnetostatic mode frequencies $ω\_{F1}$ and $ω\_{F2}$, and coupling rates to the cavity modes of gωn to the nth mode. They are coupled to each other by a cavity-mediated coupling $J$ , and for degenerate uncoupled magnetostatic modes $(δH = 0)$ new eigenmodes at $ω_{F1(2)} ± J $ result. [Lambert et. al, **PRA** 93, 021803(R) (2016)](https://link.aps.org/doi/10.1103/PhysRevA.93.021803) — Two YIG spheres are positioned at the magnetic field antinodes of the second harmonic of a transmission line cavity. Two sources, at $ω_p$ and $ω_d$ , are coupled into the cavity. The transmitted amplitude and dispersive phase shift at ωp is measured by homodyne detection. A global field, $H_0$, is applied to align the magnetization of the spheres in the propagation direction of the cavity, and tune the ferromagnetic resonance to be off-resonance with the cavity modes. The field at each sphere is adjusted by $±δH/2$ using a local coil wrapped around the cavity. (b) Energy level diagram. The lowest two cavity modes are at $ω_1$ and $ω_2$. The spatially separated magnets have magnetostatic mode frequencies $ω_{F1}$ and $ω_{F2}$, and coupling rates to the cavity modes of gωn to the nth mode. They are coupled to each other by a cavity-mediated coupling $J$ , and for degenerate uncoupled magnetostatic modes $(δH = 0)$ new eigenmodes at $ω_{F1(2)} ± J $ result. Lambert et. al, **PRA** 93, 021803(R) (2016)

The overall aim of this research project is to demonstrate non-Hermitian manipulation of cavity-magnonic devices, with particular regard to topological control permitted by the existence of the EP, and to elucidate the underlying physics of the dynamics of coupled oscillators with gain and loss. We have developed a microwave resonator in which both frequency and damping can be tuned on timescales faster than the excitations’ loss rates, and which can exhibit gain as well as loss. We couple this to magnetostatic modes in yttrium iron garnet, and carry out manipulations of the hybrid system.

Further publications

non-Hermitan Physics and Magnons

Nicholas Lambert

Research Fellow

Harald G. L. Schwefel

Associate Professor